[T] Siyam Ağları(Siamese Networks) ve Yüz Doğrulama Sistemi
Bir şeyleri görebilmek, tanıyabilmek görsel sistemimizin en önemli özelliklerinden bir tanesi. Bir elmayı, basketbol topunu veya yeni tanıştığımız bir insanı 1 veya 2 defa gördüğümüzde çok çabuk hatırlayabiliyor veya tanıyabiliyoruz. Örneğin daha önce basketbol topunu görmemiş olsanız ve ben sizlere basketbol topunun bir fotoğrafını göstersem bundan sonra basketbol topunu diğer toplardan çok rahat bir şekilde ayırt edebilirsiniz. Üstelik bu güçlü özelliğimiz ile birlikte yalnızca ayırt etmekle kalmıyor, bu bilgimizi genelleştirebiliyoruz. Örneğin top denildiği zaman yuvarlak şekilli bir nesneden bahsedildiğini biliyoruz.
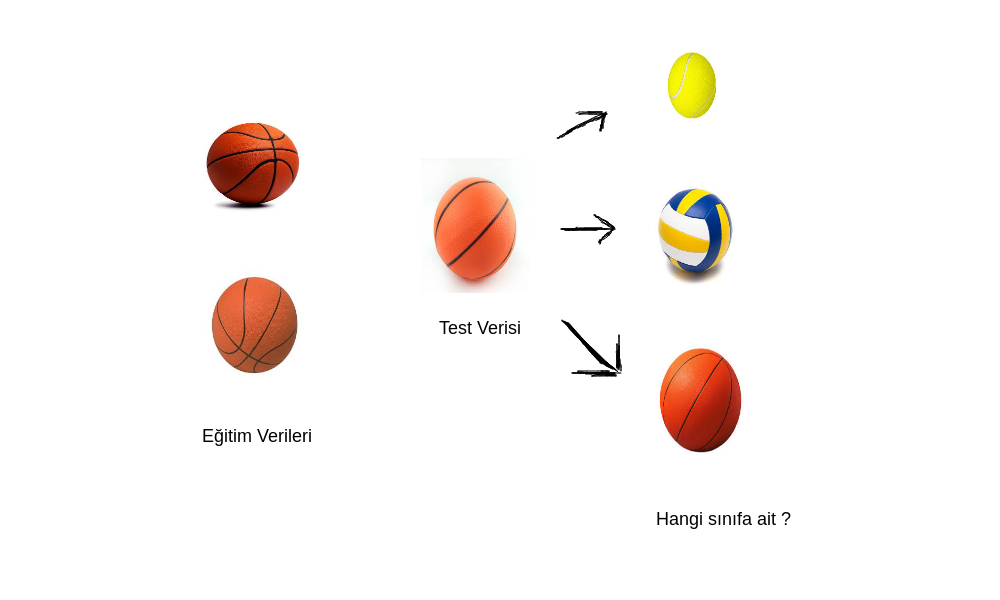
Bu eylemleri yaparken çok az veri ile yapıyoruz. Bugün bu yazıya da ilham kaynağı olan az veri kullanarak benzerlik öğrenimi(similarity learning) yapan siyam ağlarından bahsedeceğim. Devamında ise bu bilgimizi ocr-faces adresindeki verileri kullanarak, yüz doğrulama probleminde kullanacağız.
Siyam Ağları(Siamese Networks)
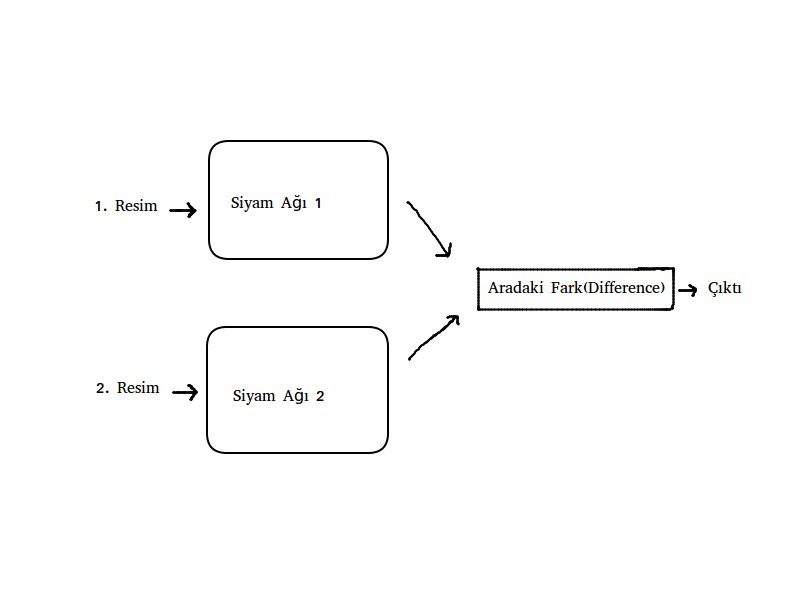
Siyam Ağları, ilk olarak 90’ların başında Bromley ve LeCun tarafından imza doğrulama(signature verification) probleminde kullanıldı.[1]
Siyam Ağları, birbirinden farklı 2 girdi(input) kabul eden birbirinin aynısı iki yapay sinir ağından oluşur. Bu sinir ağlarında parametreler paylaşılır. Yani her iki ağda da parametreler ortaktır. Bu strateji bize çok önemli bir özelliğin kapısını açıyor :
- Sinir ağlarının ürettiği tahminler tutarlıdır. Yani aynı ağırlığa sahip ağlar oldukları için birbirine çok benzeyen resimleri kullandığımızda ağın üreteceği sonuç bu iki resmin aynı kaynağa(bizim problemimizde aynı kişiye) ait olduğunu gösterecek. Aynı şekilde farklı kişilerin resimlerini verdiğimizde de aradaki fark çok olacağı için bu iki resmin farklı kişilere ait olduğunu anlamış olacağız.
Yukarıda “aradaki fark” diye bir terim kullandık, bu terimi biraz daha açmak istiyorum. Biz sinir ağına bir girdi(input) veriyoruz ve bu ağ bize girdinin encode edilmiş halini üretiyor. Aynı kişinin farklı bir resmini verdiğimizde ağımız yine bir encode edilmiş çıktı üretiyor ve biz bu iki çıktı arasındaki farka bakıyoruz. Eğer bu fark önceden belirlemiş olduğumuz bir eşik değerinin(threshold value) altında ise bu iki resmin aynı kişiye ait olduğunu anlamış oluyoruz. Eğer fark eşik değerinin üzerinde ise bu iki resim farklı kişilere aittir yorumunda bulunuyoruz.
Öklid Uzaklığı(Euclidean Distance)
Bahsetmiş olduğumuz fark kavramının matematiksel karşılığına bakalım.
\[\sqrt{\sum_{i=1}^n (x_i-y_i)^2}\]Burada \(x_i\) ve \(y_i\), modelimizin üretmiş olduğu 2 vektör. Bu vektörler 4096 elemandan oluşuyor(model oluştururken buna tekrar değineceğiz). Eleman-eleman farkların karelerini topluyoruz ve karekökünü alıyoruz.
Contrastive loss
Yapay sinir ağlarının amacı hata fonksiyonunu(loss function) mümkün olan en düşük seviyeye getirmektir. Tahmin bazlı(prediction based) hata fonksiyonlarının aksine, burada uzaklık bazlı bir hata fonksiyonu tanımlayacağız.
\[(1-Y)\frac{1}{2}{D_w}^2 + (Y)\frac{1}{2}{max(0, m-D_w)}^2\]Burada \(Y:\) eğer girdi olarak verdiğimiz resimler aynı kişiye ait ise 1, farklı kişilere ait ise 0 oluyor. \(D_w\) iki vektör arasındaki uzaklığı, \(m\) ise margin‘i temsil ediyor.
Eğer iki resim arasındaki uzaklık 0 olursa, hata fonksiyonu (0 + 0) = 0 gibi bir sonuç üretecek ve bu yüzden türevler 0 olacak. Bu sebeple modelimizi eğitememiş olacağız. Bu problemi çözmek için margin(m) değerini hata fonksiyonumuza ekliyoruz ve bir çıktı üretmeye zorluyoruz. Daha ayrıntılı bir bilgi için bu makaleyi okuyabilirsiniz.
Gerekli altyapıyı oluşturduğumuza göre asıl problemimize geçiş yapabiliriz. Bu yazıda okuyucunun evrişimsel sinir ağları(convolutional neural networks) hakkında temel bir bilgiye sahip olduğunu varsaydım. İlgili yerlerde kısa kısa açıklamalar yapacağım ama derinlemesine bir anlatım olmayacak. Detaylı anlatım için Stanford Universitesi’nin convolutional networks yazısını okuyabilirsiniz.
Kodun tamamına bu adresten erişebilirsiniz.
Kütüphaneleri ekleyerek başlayalım.
import cv2
import random
import os
import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Dense, Flatten, Input, Lambda, Dropout, Conv2D, MaxPool2D
from keras.models import Sequential, Model
from keras.optimizers import SGD
from keras.regularizers import l2, l1
import keras.backend as K
import warnings
warnings.simplefilter('ignore')
Using TensorFlow backend.
Birazdan oluşturacağımız model, girdi olarak (105, 105) boyutunda resimler alıyor. Ancak bizim indirdiğimiz resimlerin boyutu (92, 112). Bu yüzden resimleri okurken (105, 105) şeklinde tekrardan boyutlandıracağız.
Burada read_batch_imgs() isimli yardımcı bir fonksiyon yazdık. Her bir klasöre tek tek bakıp içerisindeki resimleri yüklüyoruz. Sonra da generate_images() fonksiyonunun içerisinde her bir kişinin 10 resmini alıp numpy array’ine dönüştürüyoruz. En son ise 255 ile bölerek normalizasyon işlemi yapıyoruz. Bunu yapmamızın sebebi sinir ağlarının küçük değerli girdiler ile daha iyi çalışması.
def read_batch_imgs(current_person):
imgs = []
for j in range(1, 11):
img = cv2.resize(cv2.imread('ocr_faces/s{}/{}.png'.format(current_person, j), cv2.IMREAD_GRAYSCALE),
(105, 105))
imgs += [[img]]
return imgs # Returns the original images without any normalization.
def generate_images():
train_x = []
for i in range(1, 41):
imgs = read_batch_imgs(i)
imgs = np.array(imgs).astype('float32') / 255
train_x.append(imgs)
return train_x
train_x = generate_images()
Yukarıda siyam ağlarının girdi olarak 2 resim aldığını ve aradaki farka göre çıkışın 1 veya 0 olduğundan bahsetmiştik. Eğitim verimizi oluşturmak için pozitif ve negatif örneklerden oluşan resimleri çift(pair) olarak tutuyoruz ve etiket(label) değeri için pozitif örnek ise 1, değil ise 0 yazıyoruz. En sonunda da bu çift resimleri ve etiket değerlerini numpy array’ine dönüştürüyoruz.
pairs = []
labels = []
for n in range(40):
for i in range(9):
img1, img2 = train_x[n][i], train_x[n][i + 1]
pairs += [[img1, img2]]
inc = random.randrange(1, 40)
dn = (n + inc) % 40
pairs += [[train_x[n][i], train_x[dn][i] ]]
labels += [1, 0]
pairs = np.array(pairs)
labels = np.array(labels)
Şimdi de çift olarak tuttuğumuz resimlerin boyutlarına bir bakalım.
print("Pairs shape : ", pairs.shape)
print("Labels shape : ", labels.shape)
Pairs shape : (720, 2, 1, 105, 105)
Labels shape : (720,)
Gördüğünüz üzere toplamda 720(360 pozitif, 360 negatif) adet verimiz var.
Yukarıda öklid uzaklığından ve kullanacağımız hata fonksiyonundan bahsetmiştik. Sırayla bunları tanımlayalım.
def euclidean_distance(vects):
x, y = vects
return K.sqrt(K.maximum(K.sum(K.square(x - y), axis=1, keepdims=True), K.epsilon()))
# Bu fonksiyonu modelimizin üreteceği çıktının boyutunu belirlemek için kullanacağız.
def eucl_dist_output_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
Contrastive loss : (Keras losses)
def contrastive_loss(y_true, y_pred):
margin = 1
return K.mean(y_true * K.square(y_pred) + (1 - y_true) * K.square(K.maximum(margin - y_pred, 0) ))
Son olarakta modelimizin performansını değerlendirmek için metrik fonksiyonumuzu tanımlıyoruz. (Keras metrics)
def accuracy(y_true, y_pred):
return K.mean(K.equal(y_true, K.cast(y_pred < 0.3, y_true.dtype)))
# Modelimizin eğitim ve test verisi üzerinde nasıl çalıştığını görebilmek için.
def compute_accuracy(y_true, y_pred):
pred = y_pred.ravel() < 0.3
return np.mean(pred == y_true)
İhtiyacımız olan tüm hazırlıkları yaptığımıza göre artık modelimizi tanımlamaya geçebiliriz. Modeli oluştururken bu adresteki makaleden yararlandım. Daha iyi sonuç verdiğini gözlemlediğim için 1-2 yerde değişiklik yaptım. İsterseniz siz de yeni şeyler deneyebilirsiniz. Daha iyi sonuç elde ederseniz beni de bilgilendirmeyi unutmayın :)
İlk olarak modelimizin girdi olarak hangi boyutta resimler ile çalıştığını tanımlıyoruz. Devamında ise (10, 10) boyutunda 64 filtreden oluşan Convolution katmanını tanımlıyoruz. MaxPooling katmanını ekliyoruz. pool_size için default değer (2, 2) olduğu için bir değişiklik yapmadan bırakıyoruz ve son olarakta Dropout() katmanını ekliyoruz. Bu yapıyı filtrenin boyutlarını düşürerek ve sayısını arttırarak 2 kez tekrarlıyoruz.
En son Convolution katmanından çıkan çıktıyı düz bir vektör haline getiriyoruz ve 4096 birimden(unit) oluşan Dense katmanına bağlıyoruz. Öklid uzaklığını tanımlarken 2 vektörümüzün olduğunu ve 4096 elemandan oluştuğundan bahsetmiştik. Bunun sebebi burada tanımlamış olduğumuz Dense katmanı. Aktivasyon fonksiyonu olarak bütün model boyunca ReLU, son Dense katmanında ise sigmoid kullandık.
Layers : Tüm bu katmanlar ile ilgili merak ettiğiniz yerler olursa Keras’ın dökümantasyonuna da bakabilirsiniz.
input_shape = (1, 105, 105)
def base_model_cnn(input_shape):
inp = Input(shape=input_shape)
x = Conv2D(64, (10, 10), activation='relu', data_format='channels_first')(inp)
x = MaxPool2D()(x)
x = Dropout(0.25)(x)
x = Conv2D(128, (7, 7), activation='relu')(x)
x = MaxPool2D()(x)
x = Dropout(0.25)(x)
x = Conv2D(256, (4, 4), activation='relu')(x)
x = MaxPool2D()(x)
x = Dropout(0.25)(x)
x = Conv2D(512, (4, 4), activation='relu')(x)
x = Flatten()(x)
x = Dense(4096, activation='sigmoid')(x)
return Model(inp, x)
Şimdi de ortak olarak kullanılacak sinir ağımızı tanımlayalım. Dikkat ettiyseniz ikinci bir ağ tanımlamadık. Daha önce bahsettiğimiz üzere aynı sinir ağını kullanacağız. Modelimizdeki ağırlıklar 2 kısımda da paylaşılacak. Girdi olarak 2’li çiftler olarak resimleri vereceğimizden de bahsetmiştik. Burada Lambda katmanını kullanarak modelimizin ürettiği ikili çıktılara, öklid uzaklığı(euclidean distance) fonksiyonunu uygulayacağımızı tanımlıyoruz. Son olarakta Model() kullanarak, modelimizi tanımlıyoruz.
Kısaca modelimiz, girdi olarak 2 resim alıyor ve çıktı olarakta bu 2 resim arasındaki uzaklığı döndürüyor. Bu uzaklık eğer belirli bir eşik değerinin altında ise(bizim örneğimizde 0.3) “bu iki resim aynı kişiye aittir” tahmininde bulunuyoruz.
input_a = Input(shape=input_shape)
input_b = Input(shape=input_shape)
base = base_model_cnn(input_shape)
processed_a = base(input_a)
processed_b = base(input_b)
distance = Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([processed_a, processed_b])
model = Model([input_a, input_b], distance)
Modelimizin, optimizasyon için adam, hata fonksiyonu olarakta yukarıda tanımladığımız contrastive loss fonksiyonunu kullanacağını belirtiyoruz. Performansını değerlendirmek içinde metrics’in içerisine accuracy fonksiyonunu yazıyoruz. Son olarakta modelimizin genel bir görüntüsünü bakmak için model.summary() fonksiyonunu kullanıyoruz.
model.compile(optimizer='adam', loss=contrastive_loss, metrics=[accuracy])
model.summary()
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 1, 105, 105) 0
__________________________________________________________________________________________________
input_2 (InputLayer) (None, 1, 105, 105) 0
__________________________________________________________________________________________________
model_1 (Model) (None, 4096) 28400832 input_1[0][0]
input_2[0][0]
__________________________________________________________________________________________________
lambda_1 (Lambda) (None, 1) 0 model_1[1][0]
model_1[2][0]
==================================================================================================
Total params: 28,400,832
Trainable params: 28,400,832
Non-trainable params: 0
__________________________________________________________________________________________________
Modelimizi eğitmeye geçmeden önce elimizdeki resim çiftlerini eğitim ve sınama verisi olarak ayıracağız. Ben %80’e %20’lik bir ayrım yaptım. %80 üzerinde eğitim yapacağız ve %20 üzerinde de modelimizi test edeceğiz. train_test_split
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(pairs, labels, test_size=0.2, random_state=42)
Ve artık modelimizi eğitebiliriz. Burada epoch, modelimizin kaç defa eğitim verisi üzerinden geçeceği. Ben 40 olarak tanımladım. Batch_size, bir seferde modelimizin kaç resim üzerinde eğitileceğini belirtiyor. Ben 64 olarak tanımladım. Son olarakta eğitim verimizin yüzde kaçını validation için kullanacağımızı belirtiyoruz. Ben %20’lik bir ayrım yaptım.
Yukarıda bahsettiğim bütün değerler, farklı deneme ve gözlemlerim sonucu oluştu. Daha iyileri de pek tabii ki bulunabilir.
history = model.fit([train_x[:, 0], train_x[:, 1]], train_y, epochs=40, batch_size=64, validation_split=0.2)
Modelimizi eğittik. Çıktının çok uzun olmasından dolayı göstermemeyi tercih ettim. Şimdi de eğitim verisi ve daha önce ayırmış olduğumuz test verisi üzerinde nasıl bir performans göstereceğimize bakalım.
preds = model.predict([train_x[:, 0], train_x[:, 1]])
acc = compute_accuracy(train_y, preds)
print("Train accuracy : ", acc)
preds = model.predict([test_x[:, 0], test_x[:, 1]])
acc = compute_accuracy(test_y, preds)
print("Test accuracy : ", acc)
Train accuracy : 0.9444444444444444
Test accuracy : 0.9219444444444444
Gördüğünüz üzere,
* Eğitim verisi üzerinde %94.4
* Test verisi üzerinde %92'lik bir doğruluk elde ettik.
Son olarakta modelimizin ağırlıklarını kaydedelim.
model.save_weights('model_weights.h5')
Evet yazının sonuna geldik. Yaptıklarımızı özetlemek gerekirse :
- Öncelikle resimleri (105, 105) olarak tekrardan boyutlandırdık.
- Daha sonra bu resimlerden 360 pozitif, 360 negatif olacak şekilde verimizi oluşturduk.
- Sonrasında bu veriyi %80-%20 şeklinde eğitim ve test verisi olarak ayırdık.
- Modelimizi tanımladık.
- Modelimizi eğittik.
- Test verisi üzerinde doğruluğu kontrol ettik.
Yazımda yanlış olduğunu düşündüğünüz yerleri lütfen belirtmeyi unutmayın. Teşekkürler!
Kaynaklar :